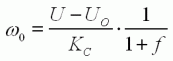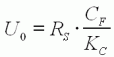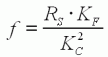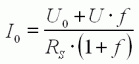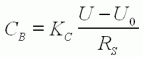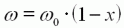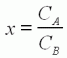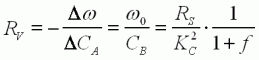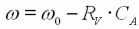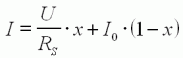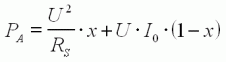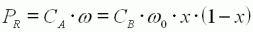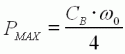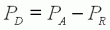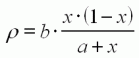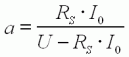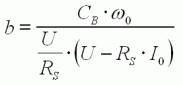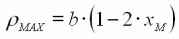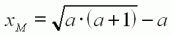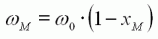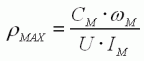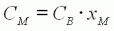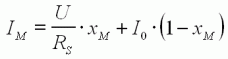| (7) | 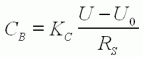 | CB
est le couple de blocage : c'est le couple maximal appliqué par le
moteur, rotor bloqué. |
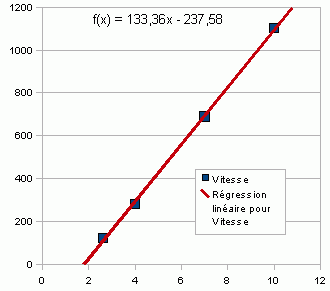
| (8) | 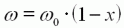 | 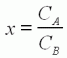 | La vitesse du moteur
diminue linéairement avec la charge. On exprime cette charge une valeur sans dimension x=CA/CB, qui varie de 0 à vide jusqu'à 1 au blocage du rotor. CA est le couple résistant
que la charge soumet à l'arbre moteur. |
| (9) | 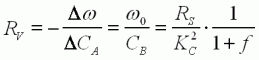 | 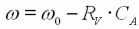 | La pente RV de
cette chute de vitesse en fonction du couple résistant CA est la constante
de régulation de vitesse
du moteur qui s'exprime en rad/(s.N.m). Plus cette constante est
faible, plus le moteur "tient la charge". C'est un bon indicateur de
performance pour nos modèles. |
| (10) |
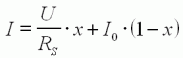 |
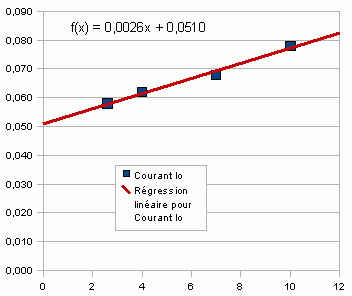
Le courant I
consommé en charge par le moteur croît linéairement avec la charge x . Il de I0 à vide (x=0) jusqu'à U/RS au blocage du rotor (x=1) . |
| (11) |
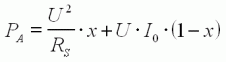
|
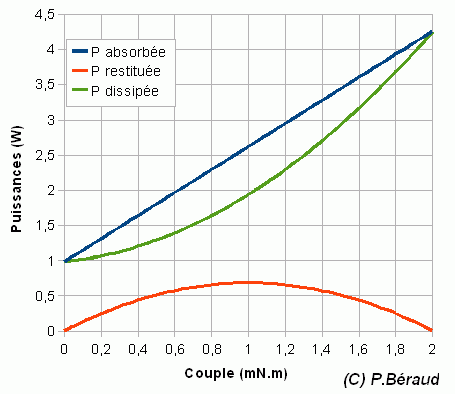
Puissance électrique (en W) absorbée par le moteur.
|
| (12) |
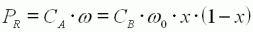
|
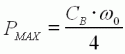
| La puissance mécanique PR
(en W) restituée sur l'arbre est
nulle à vide (x=0)
et rotor bloqué (x=1)
. Elle est maximale (PR=PMAX)
lorsque la charge fait chuter la
vitesse de moitié (x=1/2 , ω=ω0/2). |
| (13) | 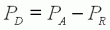 |
La puissance PD=PA-PR, qui rassemble toutes les pertes de puissance dans le moteur, est dissipée sous forme de chaleur. Cette puissance (donc
l'échauffement du moteur) croît avec la charge x, d'abord
modérément jusqu'à mi-charge (x≈0.5),
puis beaucoup plus rapidement ensuite. |
| (14) | 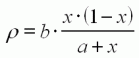
Mise à jour du 8/02/2009 : La définition de la constante a a été modifiée depuis la dernière version | 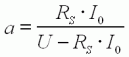
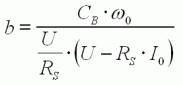
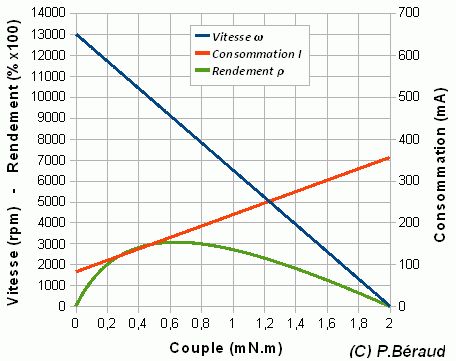
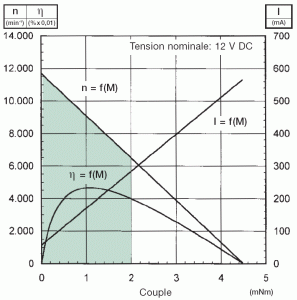
| Le rendement ρ=PR/PA est
le rapport de la puissance
mécanique restituée divisée par la puissance électrique absorbée.
Variant entre 0 et 1, il exprime l'aptitude de moteur à transformer la
puissance électrique qui lui est fournie en puissance mécanique fournie
à la charge. Il varie en fonction du régime et passe par un maximum
(voir (15) ci-dessous) généralement situé vers les 2/3 de la vitesse à
vide.
Les paramètre a
et b (sans dimension) représentent l'influence sur le rendement de toutes les
pertes interne au moteur. |
| (15) |
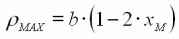
|
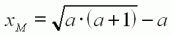
|
Le rendement ρ atteint un maximum ρMAX pour une charge particulière xM exprimée ici en fonction de a . |
| (16) |
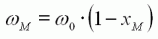
|
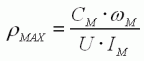
|
Expression complète du régime (vitesse, couple, courant) donnant le rendement maximal.
Une fois ces valeurs connues, il est possible de calculer simplement ρMAX selon l'expression ci-contre. |
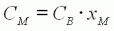
|
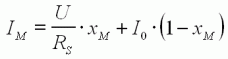
|
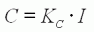
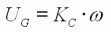
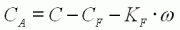
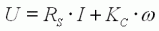
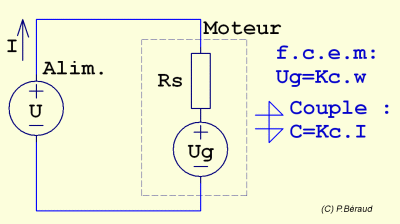 Le schéma ci-contre représente une
modélisation
électrique simplifié du moteur (partie encadrée), alimenté par un
générateur de tension
Le schéma ci-contre représente une
modélisation
électrique simplifié du moteur (partie encadrée), alimenté par un
générateur de tension