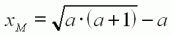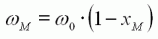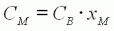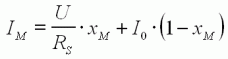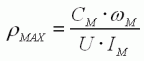| Détail des calculs |
Dernière
mise à jour :
18/02/2009
© P.Béraud 2009 |
- Fonctionnement à vide
- Fonctionnement en charge
- Puissances mises en jeu
- Rendement
La page Théorie
moteur , consacrée à la modélisation des moteurs à courant
continu et aimant permanent, donne directement sans aucune
démonstration une série d'équations qui décrivent le comportement du
moteur sous toutes les conditions de charge ou d'alimentation.
Les lecteurs curieux de trouver l'origine de ces équations, ou désireux
de vérifier les calculs, trouveront ici les calculs intermédiaires. Les
notations sont inchangées.
Rappelons les 4 équations de départ :
| (1) |
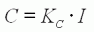 |
C
(en N.m) est le
couple généré sur le rotor, I
(en A) l'intensité du courant, et Kc
(en N.m/A) la constante de couple du moteur. Cette constante est
proportionnelle au flux magnétique dans l'induit. |
| (2) |
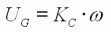 |
UG
(en V) est la f.c.e.m développée dans l'induit et ω (en
rad/s) la vitesse
angulaire.
Kc
(en N.m/A) est toujours la constante de couple du
moteur, comme dans l'équation (1).
Remarque : On s'attendrait ici à
exprimer Kc en (V.s/rad) pour satisfaire à l'homogénéité de l'équation.
Aucune contradiction portant, les (V.s/rad) et les (N.m/A) sont deux
unités équivalentes. |
| (3) |
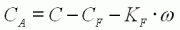 |
Pour
obtenir le couple CA
(en N.m)
disponible sur l'arbre, il faut déduite de C
divers termes de
pertes :
- Un couple de frottement CF
indépendant de
la vitesse (frottement cinématique). Il correspond à la légère
résistance que l'on peut ressentir en faisant tourner le rotor à la
main.
On peut aussi intégrer dans ce terme d'autres
pertes équivalentes à un couple constant (ou à une perte de
puissance proportionnelle à la vitesse).
- L'autre terme de couple KF.ω
correspond à
un frottement visqueux, proportionnel à la vitesse. On peut aussi
intégrer dans ce terme d'autres pertes équivalentes à un
couple proportionnel à la vitesse (ou à une perte de puissance
proportionnelle au carré
de la vitesse).
|
| (4) |
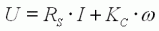 |
C'est
l'application de la loi des mailles dans le circuit électrique du
schéma ci-dessus. |
Ces 4 équations de base nous permettent de reconstituer le
comportement
du moteur dans toutes les conditions de charges et d'alimentation.
Fonctionnement à vide
Le
moteur alimenté sous la tension U
est parcouru par le courant I0.
Sa
vitesse à vide vaut ω0,
et le couple soumis à l'arbre est nul : CA=0.
D'après
(3) et (1) : 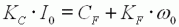 donc
donc 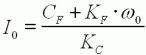
Par
ailleurs, d'après (4) : 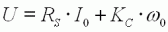 donc
donc 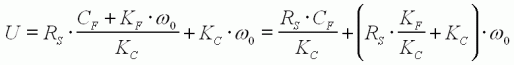
On en déduit : 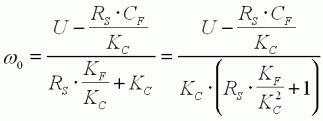
Nous sommes arrivés à l'équation (5) :
Calcul
du courant à vide : En réintroduisant l'expression de ω0
dans celle de I0
:
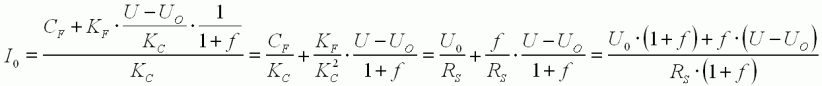
D'où
l'équation (6) :
| (6) |
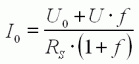 |
Fonctionnement en charge
Le moteur étant toujours alimenté sous la tension U,
on relie cette
fois à l'arbre une charge qui lui applique un couple résistant CA.
La
vitesse diminue et passe à ω,
et le courant consommé I
augmente.
En
augmentant de plus en plus la
charge, la vitesse finit par s'annuler (rotor bloqué). Le couple
atteint une valeur CB
appelée couple de blocage.
D'après
(3) : 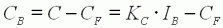
D'après
(4) : 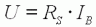
On
en déduit en utilisant (5) : 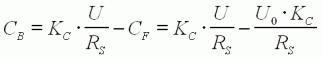
d'où
l'équation (7) :
| (7) |
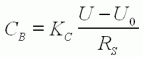
|
On va maintenant définir la
charge du
moteur par un paramètre x=CA/CB
sans dimension. Sa valeur varie de 0
(à vide) jusqu'à 1
(blocage).
D'après (1) et (3) : 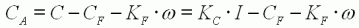 , d'où :
, d'où : 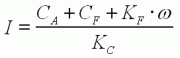
En substituant l'expression
de I
dans (4) :
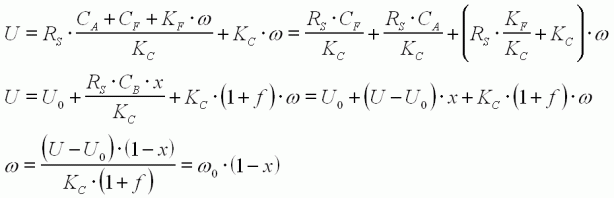
On aboutit à l'équation (8)
qui donne
la vitesse en charge :
| (8) |
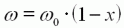 avec
avec
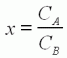
|
L'équation (8) montre une
propriété
importante : la vitesse décroît linéairement en fonction de la
charge. La pente de cette variation représente une caractéristique
importante du moteur (elle indique comment le moteur « tient
la
charge ») : C'est la constante de régulation de vitesse RV.
Elle est d'autant plus faible que le moteur est performant. Elle
s'exprime en rad/(s.N.m) dans le système international d'unités, ou
en tour/mn/(mN.m) en unités plus usuelles.
| (9) |
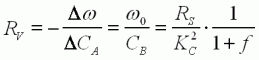 et
et
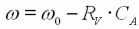
|
Calcul du courant en charge : On réintroduit l'expression de
ω
(8) dans celle de I :
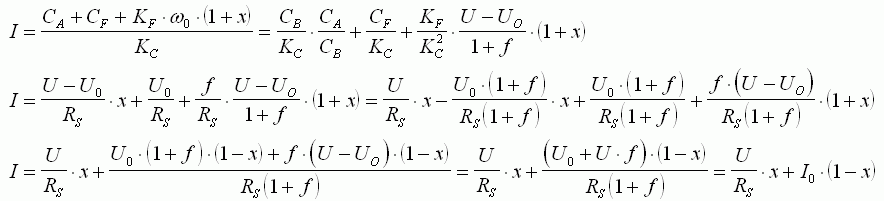
Nous sommes arrivés à l'expression du courant en fonction de la
charge (équation (10)) : Le courant varie linéairement entre I0 à
vide (x=0) jusqu'à U/RS au blocage (x=1).
| (10) |
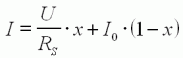
|
Puissances mises en jeu
Tout d'abord, la puissance électrique PA=U.I absorbée
par le moteur découle directement de (10) :
| (11) |
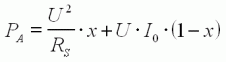
|
Ensuite, la puissance mécanique PR=CA.ω
restituée sur l'arbre :
D'après (8) : 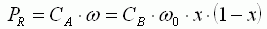
Cette équation s'annule en x=0
(fonctionnement à vide) et x=1 (rotor bloqué) et possède une
caractéristique parabolique avec un maximum en x=1/2. La puissance
restituée est maximale (PMAX) lorsque la charge fait chuter la
vitesse de moitié.
| (12) |
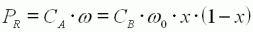 et et 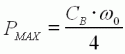
|
Puissance PD=PA-PR dissipée par le
moteur : Elle rassemble toutes les pertes de puissance dans le moteur
et est responsable de son échauffement. Cette puissance (donc
l'échauffement du moteur) croît avec la charge x, d'abord
modérément jusqu'à mi-charge (x≈0.5),
puis très rapidement ensuite.
| (13) |
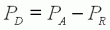
|
Rendement
Le rendement ρ=PR/PA
du moteur représente son aptitude à transformer la puissance
électrique fournie en puissance mécanique restituée sur l'axe. Il
vaudrait 1 pour un moteur idéal.
D'après (11) et (12) :
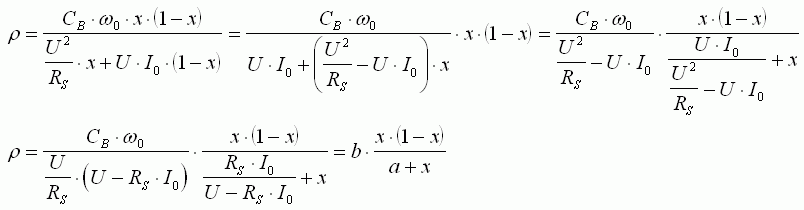
Nous sommes arrivés à une expression du rendement :
Le rendement est nul à vide (x=0) et
rotor bloqué (x=1), et passe par un maximum à un régime
particulier. Recherchons ce maximum :
On cherche le zéro de la dérivée :
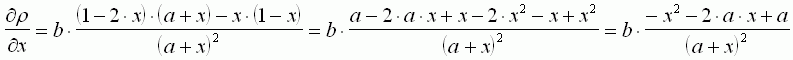
Les racines x1 et x2 du numérateur
sont :
Discriminant : 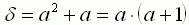
Racines : 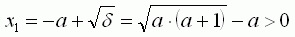 et
et 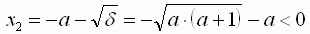
Seule la première racine est valable
(appelons la xM), la seconde est négative.
On en déduit la valeur du rendement au
maximum :
On remarque dans l'expression de la
dérivée de ρ que celle-ci s'annule lorsque : 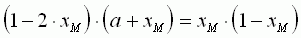
En reportant dans l'expression de ρ :
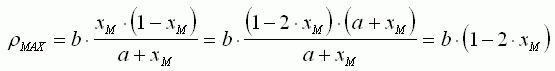
Nous connaissons maintenant le
rendement maximal et la charge correspondante xM :
| (15) |
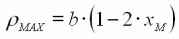 avec : avec : 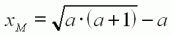
|
Nous pouvons également exprimer le
point de fonctionnement (vitesse, couple, courant) correspondant, en
appliquant à xM les équations (8) et (10) :
| Vous
avez remarqué une erreur, vous souhaitez formuler des
remarques, critiques (constructives), encouragements : |
Ecrivez-moi
! |
Visites depuis le 1/02/2009 : 58383 -
Page réalisée à l'aide de 
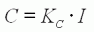
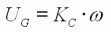
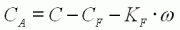
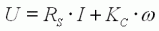
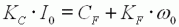 donc
donc 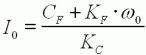
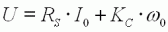 donc
donc 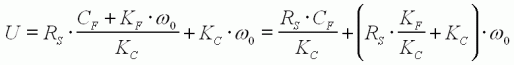
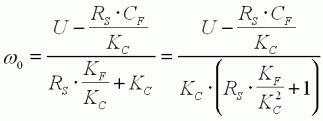
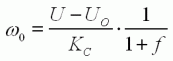 avec :
avec : 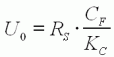 et
et 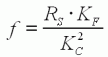
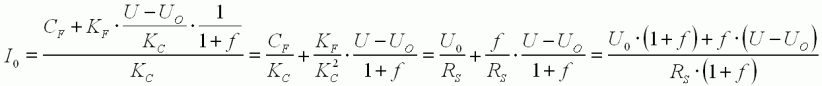
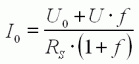
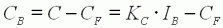
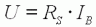
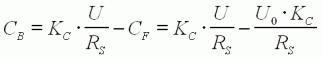
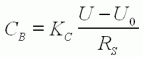
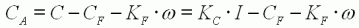 , d'où :
, d'où : 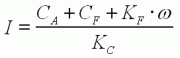
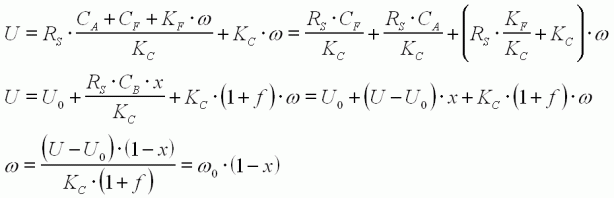
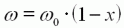 avec
avec
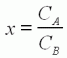
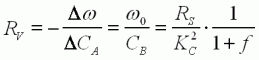 et
et
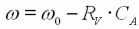
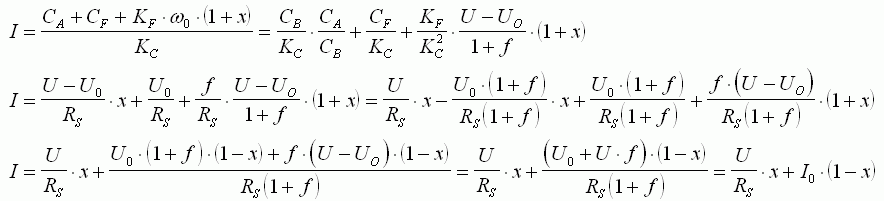
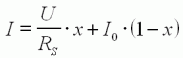
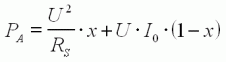
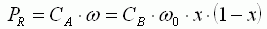
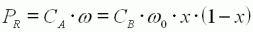 et
et 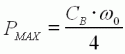
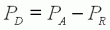
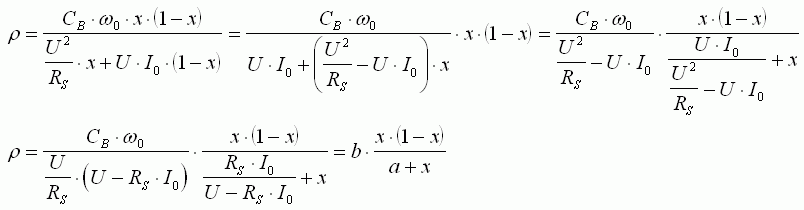
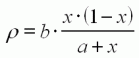 avec :
avec : 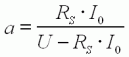 et
et 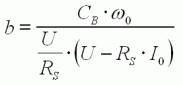
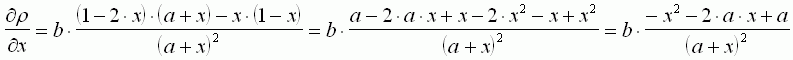
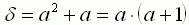
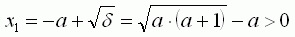 et
et 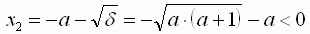
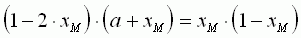
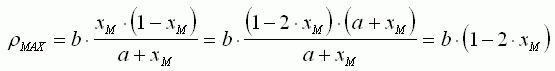
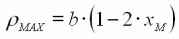 avec :
avec :